I’ll describe one way to go from a boot sector loaded by the BIOS with the CPU in 16-bit real mode to the CPU set up in 64-bit long mode. The setup is pretty bare-bones and there’s tons more to do.
To follow along, you need the Intel 64 and IA-32 Architectures Software Developer’s Manual, an assembler (I used nasm), and QEMU. If you don’t have an x86_64 CPU, you should still be able to run everything I describe by emulating an x86 CPU in QEMU. I assume you know x86 assembly and the syntax that nasm uses. I like the nasm tutorial by Ray Toal for getting started.
I was surprised by how readable some of the Intel manual is. The initial chapters in volume 1 do a really good job at providing an overview of the system and explaining the terms used throughout the other volumes. But volume 3: System Programming Guide is most relevant to this discussion. There is an overview of all the operating modes in volume 3, section 2.2 Modes of Operation. The path we’re taking is highlighted in red.
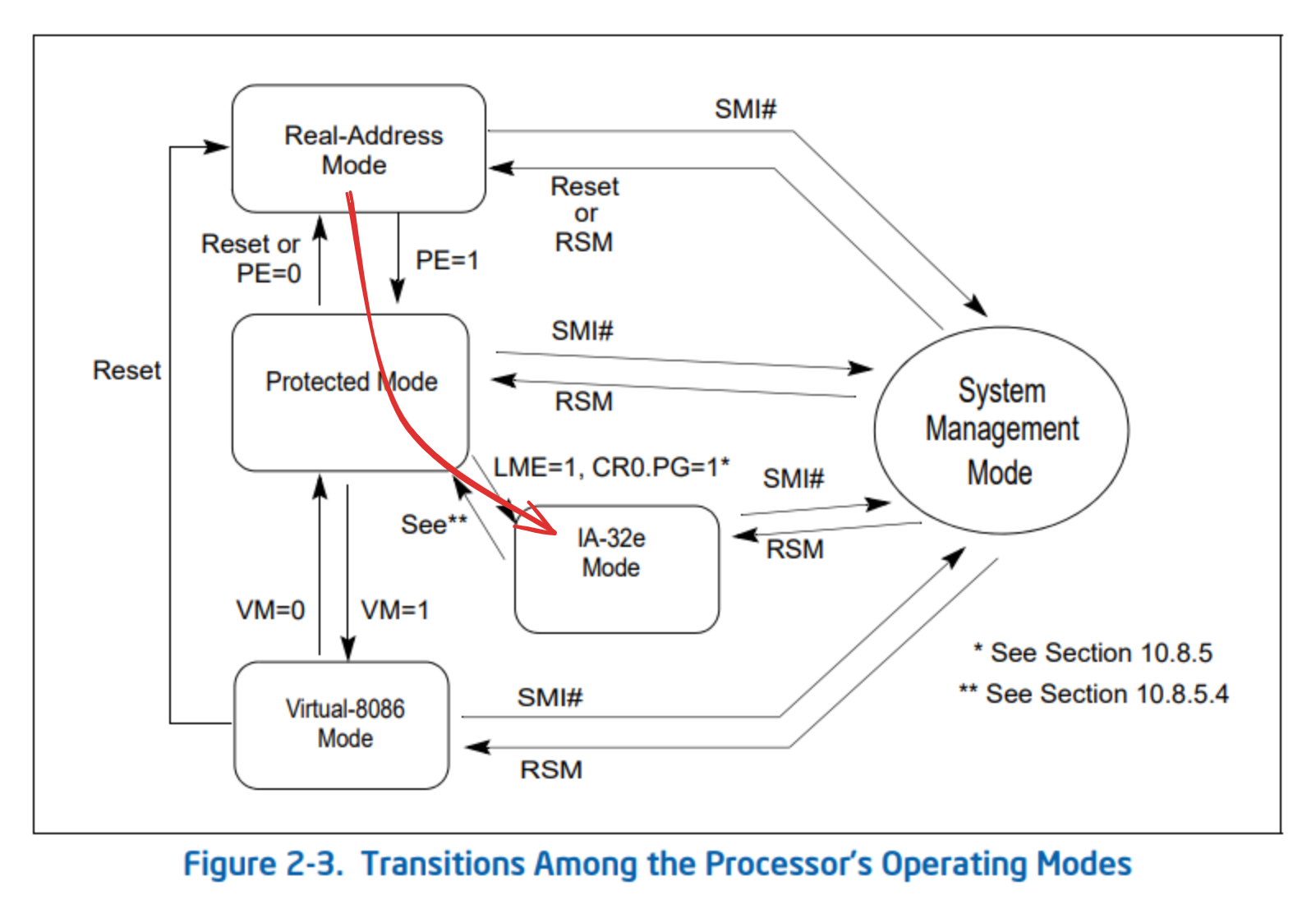
For everything up to 32-bit mode, take a look at “Writing a Simple Operating System – from Scratch”. It’s unfinished but still very good.
Starting Point: BIOS
After a reset, the x86 CPU is in “real mode”. That mode has a default operand size of 16 bits. You get a 20-bit address space and thus the ability to address 1MB of memory by using segmentation. Real mode is pretty much a backward compatibility mode for the Intel 8086 chip from 1978.
After the BIOS the first code that runs is that in the boot sector. The BIOS
searches the system for a disk where the first sector ends in the magic
number 0xaa55 (i.e., the byte 0x55 followed by the byte 0xaa). It loads
that “boot sector” to memory at address 0x7c00.
So the BIOS gives us 512 bytes to work with. We need to use these bytes in order to bootstrap the rest of the bootloader. One can fit a surprising amount of stuff in 512 bytes, but it’s easiest to just load some more data from disk first. Fortunately, routines defined by the BIOS remain available to us as long as we’re in real mode.
Boot Sector Setup
Let’s set up a simple boot sector. It will just print a message to the screen using BIOS routines and then hang. This way, we know that the tooling works.
This is the assembly we need:
;; src/boot_sector.s
section .boot_sector
global __start
[bits 16]
__start:
mov bx, hello_msg
call print_string
end:
hlt
jmp end
;; Uses the BIOS to print a null-termianted string. The address of the
;; string is found in the bx register.
print_string:
pusha
mov ah, 0x0e ; BIOS "display character" function
print_string_loop:
cmp byte [bx], 0
je print_string_return
mov al, [bx]
int 0x10 ; BIOS video services
inc bx
jmp print_string_loop
print_string_return:
popa
ret
hello_msg: db "Hello, world!", 0
Plus this Makefile:
# Makefile
.PHONY: all clean boot
NASM := nasm -f elf64
BUILD_DIR := build
SRC_DIR := src
SRC := $(wildcard $(SRC_DIR)/*.s)
OBJS := $(patsubst $(SRC_DIR)/%.s, $(BUILD_DIR)/%.o, $(SRC))
BOOT_IMAGE := $(BUILD_DIR)/boot_image
all: $(BOOT_IMAGE)
boot: $(BOOT_IMAGE)
qemu-system-x86_64 -no-reboot -drive file=$<,format=raw,index=0,media=disk
$(BOOT_IMAGE): $(BUILD_DIR)/linked.o
objcopy -O binary $< $@
$(BUILD_DIR)/linked.o: $(OBJS)
ld -T linker.ld -o $@ $^
$(BUILD_DIR)/%.o: $(SRC_DIR)/%.s
@mkdir -p $(dir $@)
$(NASM) $< -o $@
clean:
$(RM) -r $(BUILD_DIR)
The linker script linker.ld is important because it makes sure that
the code in our boot sector is relocated to the right address in the
final image. Specifically, the bootloader loads the boot sector to
address 0x7c00 in memory. So that’s the base address to relocate
the boot sector to. In addition, the linker will add the magic number
at the end of the boot sector. Other guides I’ve seen do both the offset
and the magic number inside the boot sector assembly source file by using
features of the assembler, but that’s somewhat hackish.
# linker.ld
MEMORY
{
boot_sector (rwx) : ORIGIN = 0x7c00, LENGTH = 512
}
ENTRY(__start)
SECTIONS
{
.boot_sector : { *(.boot_sector); } > boot_sector
.bootsign (0x7c00 + 510) :
{
BYTE(0x55)
BYTE(0xaa)
} > boot_sector
}
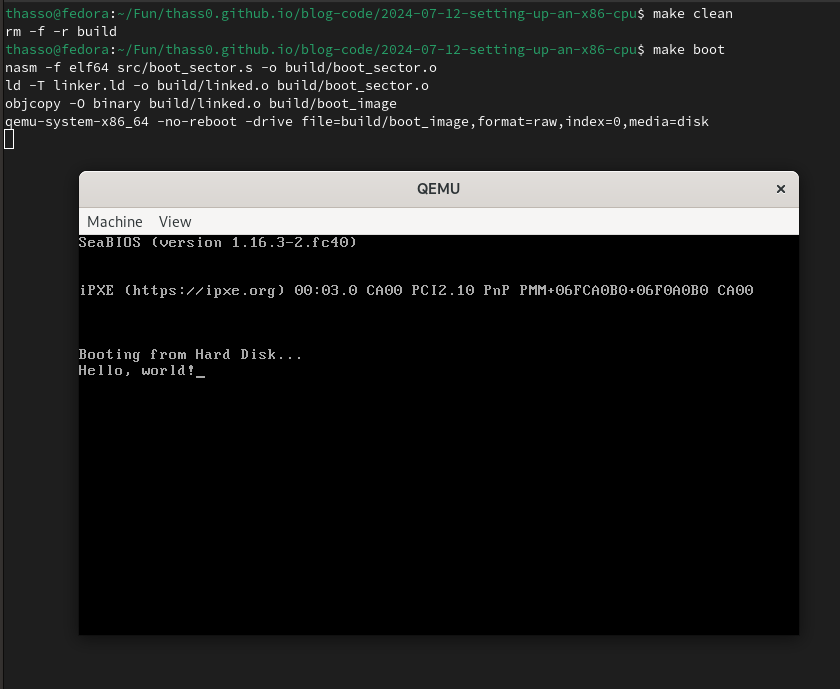
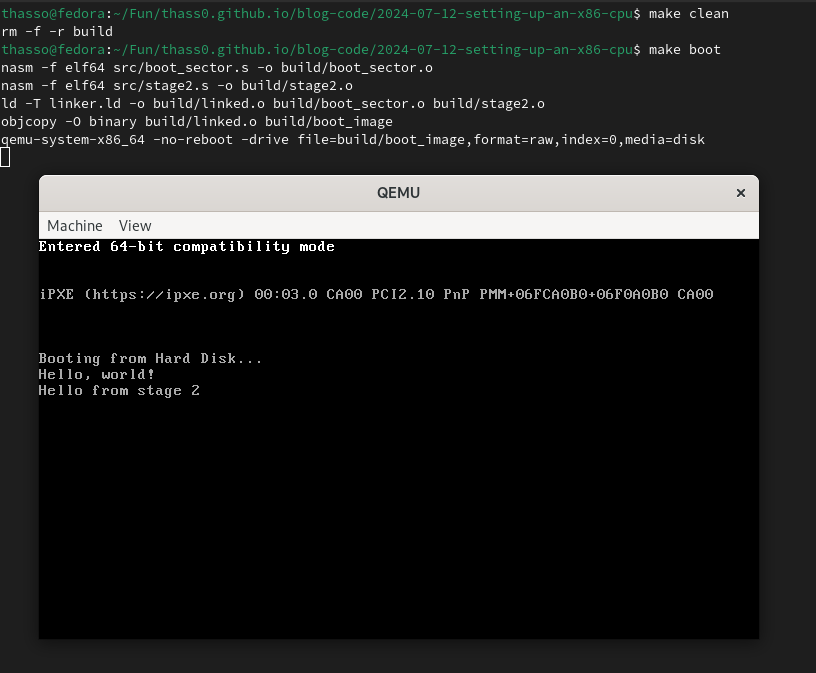
Running make boot should result in a QEMU window and
the “Hello, World!” message should be displayed.
Stage 1 – Loading Stage 2 From Disk
We can split the bootloader into two stages. Stage 1 is the code in the boot sector. It is everything that the BIOS loads for us. The sole purpose of stage 1 is to load stage 2 into memory. Stage 1 does this by using BIOS-provided routines to load stage 2 into memory.
In stage 2, we’ll switch from 16-bit real mode to 32-bit protected mode. In protected mode, we can’t use BIOS routines anymore. Without BIOS routines, loading sectors from a disk would become much more involved. So we’ll load a number of sectors from disk into memory and hope for the best. Of course, this is an unsafe technique, but it works for now.
This is how one can access the disk using BIOS. There’s an osdev.org page on this.
;; src/boot_sector.s
;; ...
__start:
;; ...
mov si, disk_address_packet
mov ah, 0x42 ; BIOS "extended read" function
mov dl, 0x80 ; Drive number
int 0x13 ; BIOS disk services
jc error_reading_disk
ignore_disk_read_error:
SND_STAGE_ADDR equ (BOOT_LOAD_ADDR + SECTOR_SIZE)
jmp 0:SND_STAGE_ADDR
error_reading_disk:
;; We accept reading fewer sectors than requested
cmp word [dap_sectors_num], READ_SECTORS_NUM
jle ignore_disk_read_error
mov bx, error_reading_disk_msg
call print_string
end:
;; ...
And at the end of boot_sector.s put this data:
;; src/boot_sector.s
;; ...
align 4
disk_address_packet:
db 0x10 ; Size of packet
db 0 ; Reserved, always 0
dap_sectors_num:
dw READ_SECTORS_NUM ; Number of sectors read
dd (BOOT_LOAD_ADDR + SECTOR_SIZE) ; Destination address
dq 1 ; Sector to start at (0 is the boot sector)
READ_SECTORS_NUM equ 64
BOOT_LOAD_ADDR equ 0x7c00
SECTOR_SIZE equ 512
hello_msg: db "Hello, world!", 13, 10, 0
error_reading_disk_msg: db "Error: failed to read disk with 0x13/ah=0x42", 13, 10, 0
Lastly we need a stage 2 to jump to and we need to update the linker script.
The Makefile remains unchanged.
;; src/stage2.s
section .stage2
[bits 16]
mov bx, stage2_msg
call print_string
end:
hlt
jmp end
print_string:
;; ...
stage2_msg: db "Hello from stage 2", 13, 10, 0
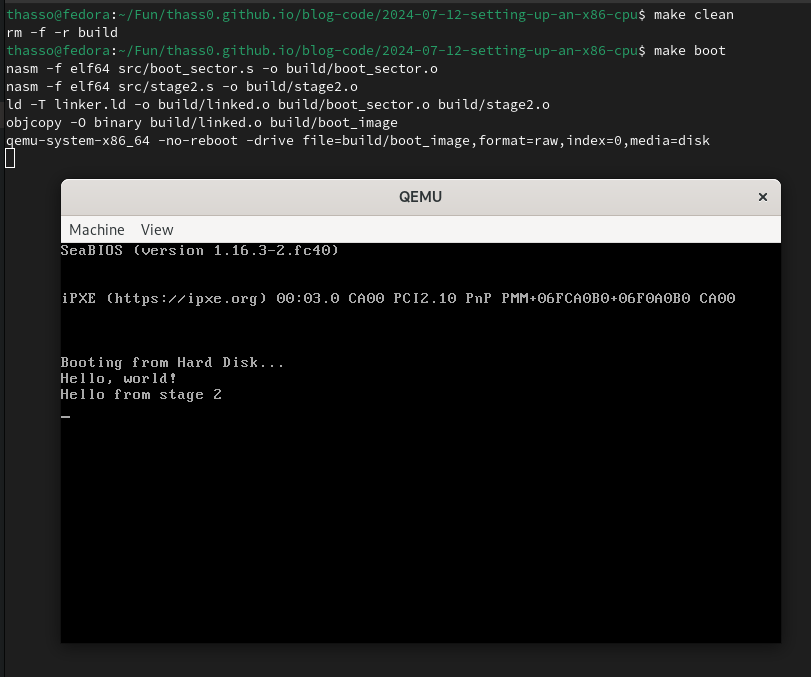
I just copied the print_string function so we can test if the jump works.
Because this specific function only works with BIOS in real mode, it won’t
be of any use to stage 2 once we have switched to protected mode.
Finally the linker script:
# linker.ld
MEMORY
{
boot_sector (rwx) : ORIGIN = 0x7c00, LENGTH = 512
stage2 (rwx) : ORIGIN = 0x7e00, LENGTH = 32768 # 512 * 64
}
ENTRY(__start)
SECTIONS
{
.boot_sector : { *(.boot_sector); } > boot_sector
.bootsign (0x7c00 + 510) :
{
BYTE(0x55)
BYTE(0xaa)
} > boot_sector
.stage2 : { *(.stage2); } > stage2
}
32-bit Protected Mode
Next, we’ll switch the CPU from real mode (16-bit) to protected mode (32-bit). In protected mode, segmentation is used by default to implement memory protection. Before switching to protected mode, you need to define a Global Descriptor Table (GDT) that contains segment descriptors for all the segments you want to define. Usually, paging is used in favor of segmentation. In fact, in 64-bit long mode, you need to use paging. But for the initial switch to protected mode, segmentation is required.
The Intel manual describes the “flat model” as a very simple segmentation model that can be implemented in the GDT. The “flat model” comprises a code segment and a data segment. Both of these segments are mapped to the entire linear address space (their base addresses and limits are identical). Using the simplest of all models is fine, since we just want to get to long mode and abandon segmentation in favor of paging.
The GDT is defined as a contiguous structure in memory. You fill a chunk of memory with the right data and give the CPU the address and the length of the memory chunk. The format of the GDT structure is described in the Intel manual.
From section “3.4.5 Segment Descriptors”:

The GDT is just an array of segment descriptors with a “null descriptor” at the start that’s used to catch invalid translations. The fields in the segment descriptor are described in detail in section “3.4.5 Segment Descriptors” of volume 3 of the Intel manual.
We define the GDT like this:
;; include/gdt32.s
;; Base address of GDT should be aligned on an eight-byte boundary
align 8
gdt32_start:
;; 8-byte null descriptor (index 0).
;; Used to catch translations with a null selector.
dd 0x0
dd 0x0
gdt32_code_segment:
;; 8-byte code segment descriptor (index 1).
;; First 16 bits of segment limit
dw 0xffff
;; First 24 bits of segment base address
dw 0x0000
db 0x00
;; 0-3: segment type that specifies an execute/read code segment
;; 4: descriptor type flag indicating that this is a code/data segment
;; 5-6: Descriptor privilege level 0 (most privileged)
;; 7: Segment present flag set indicating that the segment is present
db 10011010b
;; 0-3: last 4 bits of segment limit
;; 4: unused (available for use by system software)
;; 5: 64-bit code segment flag indicates that the segment doesn't contain 64-bit code
;; 6: default operation size of 32 bits
;; 7: granularity of 4 kilobyte units
db 11001111b
;; Last 8 bits of segment base address
db 0x00
gdt32_data_segment:
;; Only differences are explained ...
dw 0xffff
dw 0x0000
db 0x00
;; 0-3: segment type that specifies a read/write data segment
db 10010010b
db 11001111b
db 0x00
gdt32_end:
;; Value for GDTR register that describes the above GDT
gdt32_pseudo_descriptor:
;; A limit value of 0 results in one valid byte. So, the limit value of our
;; GDT is its length in bytes minus 1.
dw gdt32_end - gdt32_start - 1
;; Start address of the GDT
dd gdt32_start
CODE_SEG32 equ gdt32_code_segment - gdt32_start
DATA_SEG32 equ gdt32_data_segment - gdt32_start
Switching to protected mode is very easy now. We load the GDT pseudo-descriptor into the GDTR register so that the base address and length of our GDT are known to the system. Lastly, we do a far jump to flush the instruction pipeline.
;; src/stage2.s
section .stage2
[bits 16]
;; ...
;; Load GDT and switch to protected mode
cli ; Can't have interrupts during the switch
lgdt [gdt32_pseudo_descriptor]
;; Setting cr0.PE (bit 0) enables protected mode
mov eax, cr0
or eax, 1
mov cr0, eax
;; The far jump into the code segment from the new GDT flushes
;; the CPU pipeline removing any 16-bit decoded instructions
;; and updates the cs register with the new code segment.
jmp CODE_SEG32:start_prot_mode
[bits 32]
start_prot_mode:
;; Old segments are now meaningless
mov ax, DATA_SEG32
mov ds, ax
mov ss, ax
mov es, ax
mov fs, ax
mov gs, ax
;; ...
%include "include/gdt32.s"
Interrupts are disabled during the switch. After the entire setup is complete, interrupts can be enabled again. This would require extra setup work.
Now that we’re in protected mode, we can’t use the BIOS routines anymore. To print text, we can write straight to the VGA buffer instead.
;; src/stage2.s
;; ...
;; Writes a null-terminated string straight to the VGA buffer.
;; The address of the string is found in the bx register.
print_string32:
pusha
VGA_BUF equ 0xb8000
WB_COLOR equ 0xf
mov edx, VGA_BUF
print_string32_loop:
cmp byte [ebx], 0
je print_string32_return
mov al, [ebx]
mov ah, WB_COLOR
mov [edx], ax
add ebx, 1 ; Next character
add edx, 2 ; Next VGA buffer cell
jmp print_string32_loop
print_string32_return:
popa
ret
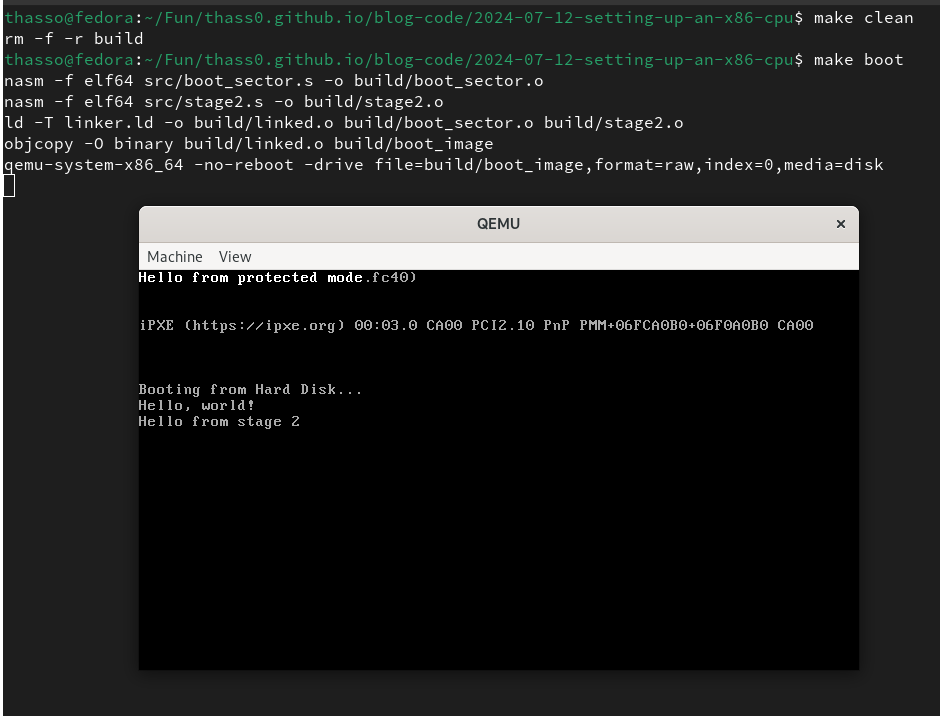
Best print something so that we know the switch worked. To do that, add a
string with the message and a call to print_string32 to the code.
The print_string32 function is super basic, so the message always shows
up in the top left corner of the display.
64-bit Long Mode
For this part, refer to “10.8.5 Initializing IA-32e Mode”. Note that Intel calls the 64-bit mode “IA-32e” while AMD refers to it as “long mode” in the AMD64 manual.
Before switching to long mode, the CPU must be in protected mode and paging must be enabled. We have protected mode now, but we are missing paging.
I love paging. It’s just very cool. But I’d do a poor job at explaining the concept itself. Philipp Oppermann’s Introduction to Paging from the “Writing an OS in Rust” blog was really useful for me personally. OSTEP also talks about paging starting chapter 18, although it doesn’t go into the specifics of paging on x86 like Philipp Oppermann’s post does.
In long mode with Physical Address Extension enabled (PAE, we’ll do that below ), a four level page table is used. The below code generates such a page table at a given address.
;; src/stage2.s
;; Builds a 4 level page table starting at the address that's passed in ebx.
build_page_table:
pusha
PAGE64_PAGE_SIZE equ 0x1000
PAGE64_TAB_SIZE equ 0x1000
PAGE64_TAB_ENT_NUM equ 512
;; Initialize all four tables to 0. If the present flag is cleared, all other bits in any
;; entry are ignored. So by filling all entries with zeros, they are all "not present".
;; Each repetition zeros four bytes at once. That's why a number of repetitions equal to
;; the size of a single page table is enough to zero all four tables.
mov ecx, PAGE64_TAB_SIZE ; ecx stores the number of repetitions
mov edi, ebx ; edi stores the base address
xor eax, eax ; eax stores the value
rep stosd
;; Link first entry in PML4 table to the PDP table
mov edi, ebx
lea eax, [edi + (PAGE64_TAB_SIZE | 11b)] ; Set read/write and present flags
mov dword [edi], eax
;; Link first entry in PDP table to the PD table
add edi, PAGE64_TAB_SIZE
add eax, PAGE64_TAB_SIZE
mov dword [edi], eax
;; Link the first entry in the PD table to the page table
add edi, PAGE64_TAB_SIZE
add eax, PAGE64_TAB_SIZE
mov dword [edi], eax
;; Initialize only a single page on the lowest (page table) layer in
;; the four level page table.
add edi, PAGE64_TAB_SIZE
mov ebx, 11b
mov ecx, PAGE64_TAB_ENT_NUM
set_page_table_entry:
mov dword [edi], ebx
add ebx, PAGE64_PAGE_SIZE
add edi, 8
loop set_page_table_entry
popa
ret
Paging supersedes segmentation for managing virtual address spaces, permissions, etc. A Global Descriptor Table with segment descriptors is still needed though, and the segment descriptors must be modified slightly to enable long mode-specific features.
This is another GDT that also implements the flat model. It’s almost identical to the GDT for protected mode. Just two bits were changed.
;; include/gdt64.s
align 16
gdt64_start:
;; 8-byte null descriptor (index 0).
dd 0x0
dd 0x0
gdt64_code_segment:
dw 0xffff
dw 0x0000
db 0x00
db 10011010b
;; 5: 64-bit code segment flag indicates that this segment contains 64-bit code
;; 6: must be zero if L bit (bit 5) is set
db 10101111b
db 0x00
gdt64_data_segment:
dw 0xffff
dw 0x0000
db 0x00
;; 0-3: segment type that specifies a read/write data segment
db 10010010b
db 10101111b
db 0x00
gdt64_end:
gdt64_pseudo_descriptor:
dw gdt64_end - gdt64_start - 1
dd gdt64_start
CODE_SEG64 equ gdt64_code_segment - gdt64_start
DATA_SEG64 equ gdt64_data_segment - gdt64_start
With the page table and the GDT in place, the switch from protected mode to long mode can be performed.
;; src/stage2.s
;; ...
start_prot_mode:
;; ...
;; Build 4 level page table and switch to long mode
mov ebx, 0x1000
call build_page_table
mov cr3, ebx ; MMU finds the PML4 table in cr3
;; Enable Physical Address Extension (PAE). This is needed to allow the switch
mov eax, cr4
or eax, 1 << 5
mov cr4, eax
;; The EFER (Extended Feature Enable Register) MSR (Model-Specific Register) contains fields
;; related to IA-32e mode operation. Bit 8 if this MSR is the LME (long mode enable) flag
;; that enables IA-32e operation.
mov ecx, 0xc0000080
rdmsr
or eax, 1 << 8
wrmsr
;; Enable paging (PG flag in cr0, bit 31)
mov eax, cr0
or eax, 1 << 31
mov cr0, eax
mov ebx, comp_mode_msg
call print_string32
;; New GDT has the 64-bit segment flag set. This makes the CPU switch from
;; IA-32e compatibility mode to 64-bit mode.
lgdt [gdt64_pseudo_descriptor]
jmp CODE_SEG64:start_long_mode
;; ...
[bits 64]
start_long_mode:
hlt
jmp start_long_mode
;; ...
%include "include/gdt64.s"
;; ...
comp_mode_msg: db "Entered 64-bit compatibility mode", 0
Again, the “success message” should show up in the top left corner. Write a small VGA driver if this annoys you.
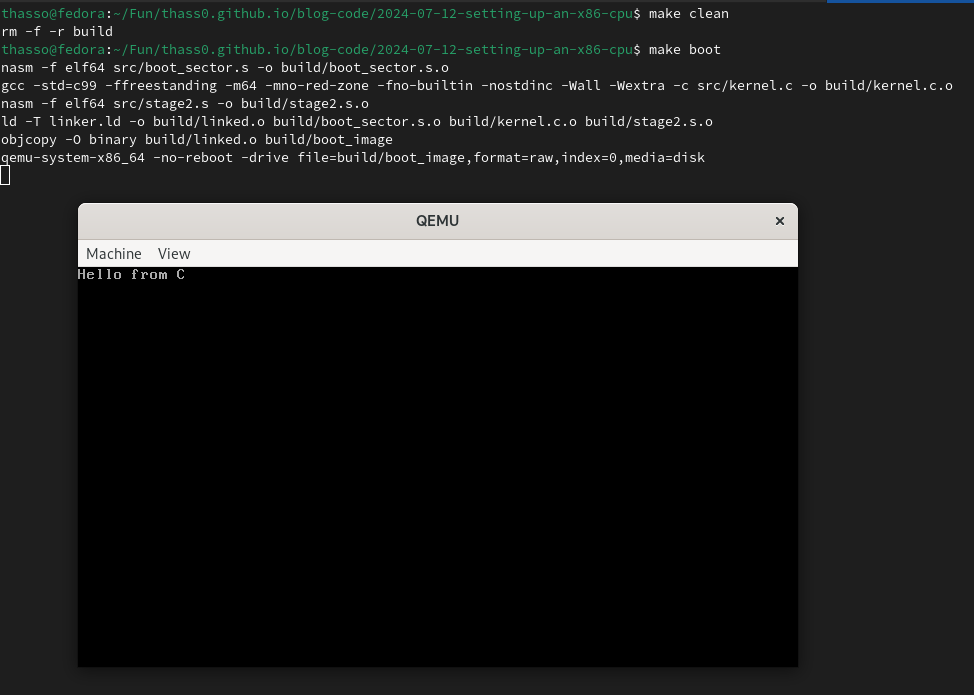
Using C
C code can easily be intergrated into this setup. E.g, this might become an OS kernel.
/* src/kernel.c */
#define VGA_COLUMNS_NUM 80
#define VGA_ROWS_NUM 25
#define ARRAY_SIZE(arr) ((int)sizeof(arr) / (int)sizeof((arr)[0]))
void _start_kernel(void) {
volatile char *vga_buf = (char *)0xb8000;
const char msg[] = "Hello from C";
int i;
for (i = 0; i < VGA_COLUMNS_NUM * VGA_ROWS_NUM * 2; i++)
vga_buf[i] = '\0';
for (i = 0; i < ARRAY_SIZE(msg) - 1; i++) {
vga_buf[i * 2] = msg[i];
vga_buf[i * 2 + 1] = 0x07; /* White on black */
}
}
Update src/stage2.s:
;; src/stage2.s
;; ...
[bits 64]
start_long_mode:
mov ebx, long_mode_msg
call print_string64
extern _start_kernel
call _start_kernel
end64:
hlt
jmp end64
;; ...
The linker script:
# linker.ld
MEMORY
{
boot_sector (rwx) : ORIGIN = 0x7c00, LENGTH = 512
stage2 (rwx) : ORIGIN = 0x7e00, LENGTH = 512
kernel (rwx) : ORIGIN = 0x8000, LENGTH = 0x10000
}
ENTRY(__start)
SECTIONS
{
.boot_sector : { *(.boot_sector); } > boot_sector
.bootsign (0x7c00 + 510) :
{
BYTE(0x55)
BYTE(0xaa)
} > boot_sector
.stage2 : { *(.stage2); } > stage2
.text : { *(.text); } > kernel
.data : { *(.data); } > kernel
.rodata : { *(.rodata); } > kernel
.bss :
{
*(.bss)
*(COMMON)
} > kernel
}
Lastly, the Makefile needs to change. Here, I only included the lines
that have changed.
# Makefile
# ...
CC := gcc
CFLAGS := -std=c99 -ffreestanding -m64 -mno-red-zone -fno-builtin -nostdinc -Wall -Wextra
# ...
SRC := $(wildcard $(SRC_DIR)/*)
OBJS := $(patsubst $(SRC_DIR)/%, $(BUILD_DIR)/%.o, $(SRC))
# ...
$(BUILD_DIR)/%.s.o: $(SRC_DIR)/%.s
@mkdir -p $(dir $@)
$(NASM) $< -o $@
$(BUILD_DIR)/%.c.o: $(SRC_DIR)/%.c
@mkdir -p $(dir $@)
$(CC) $(CFLAGS) -c $< -o $@
# ...
Cool if you actually came along this far. The code is on GitHub.
]]>