Parsing numerical expressions by recursive descent is a joy in Haskell! It is incredibly concise and elegant, yet very simple.

What we want to parse are binary expressions like 7 + 42 * 9, 2 * 3 / 4 * 5, or 8 * (10 - 6). As always, when parsing such expressions, we have to be aware of the associativity of the operators involved and of their different levels of precedence. In this case it’s simple: +, -, *, and / all associate to the left, and * and / have higher precedence than + and -.

This means that we want to turn the above expressions into the following ASTs.¹

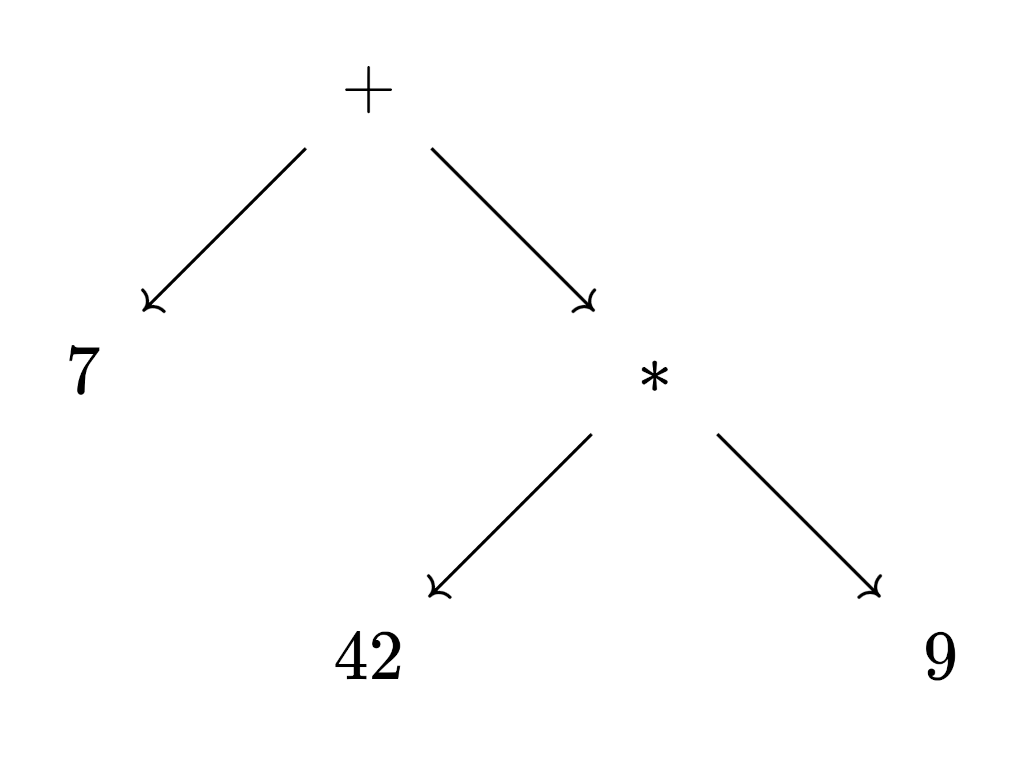
7 + 42 * 9 ⇒ 7 + (42 * 9). * has higher precedence than +, so although they both associate to the left, * binds tighter than +.

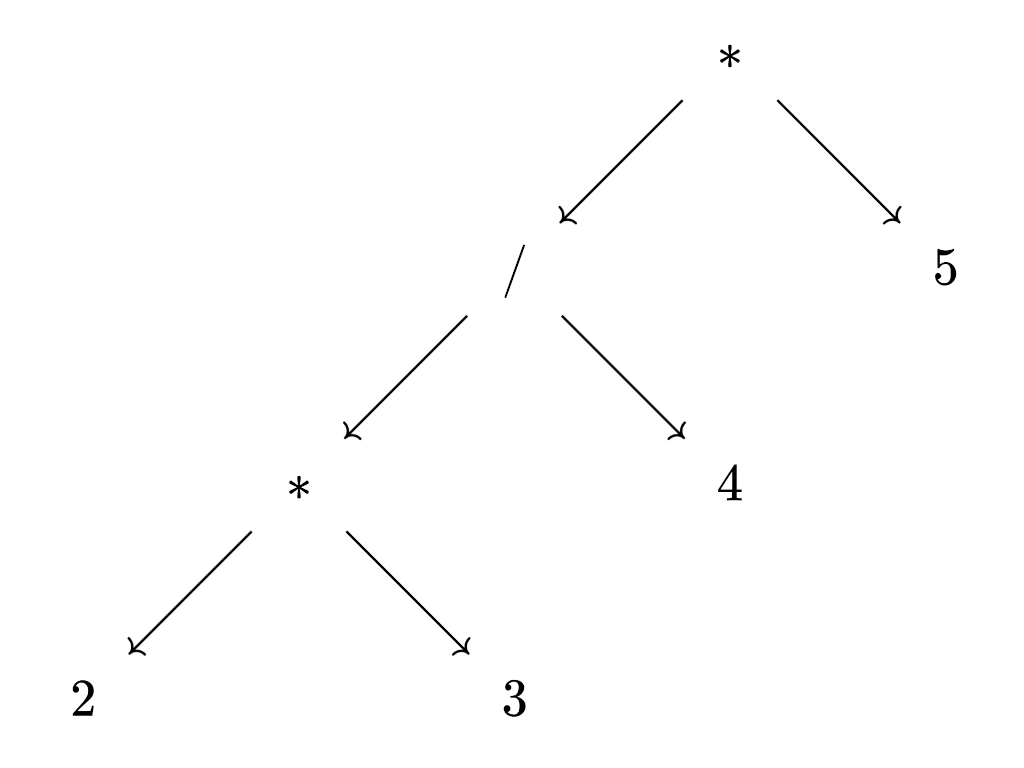
2 * 3 / 4 * 5 ⇒ ((2 * 3) / 4) * 5. * and / have the same precedence and associate to the left.

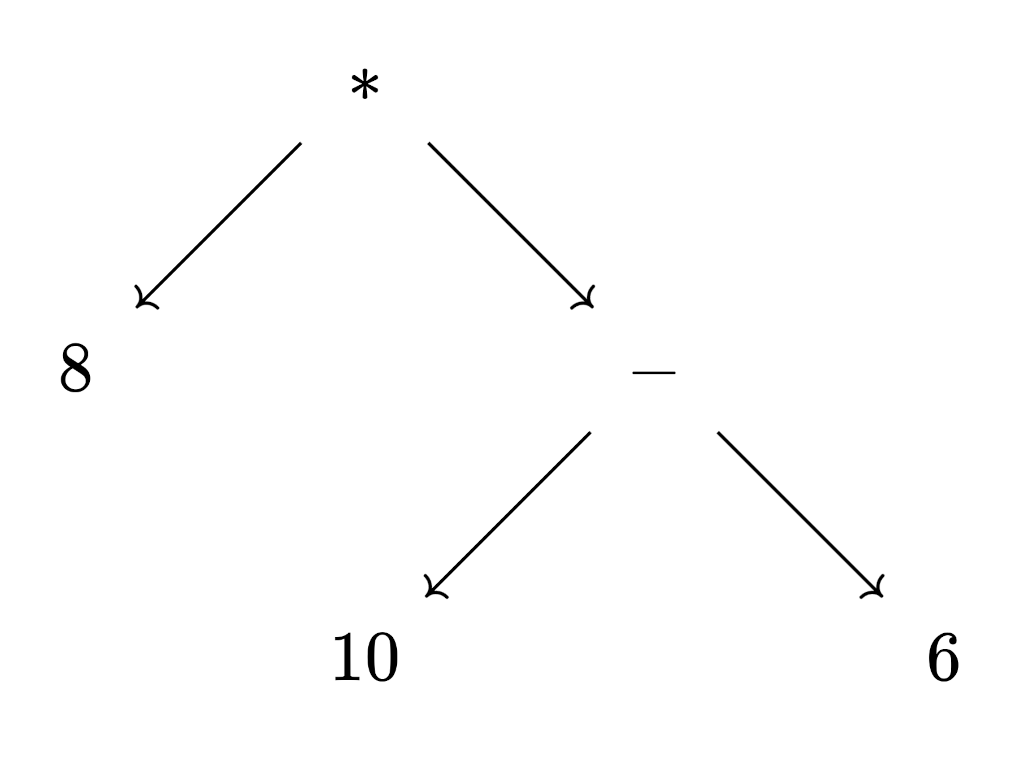
8 * (10 - 6). Parentheses have the highest precedence.

The following grammar encodes the precedence and associativity constraints above. It is also not left-recursive, and can be used in a recursive descent parser.²

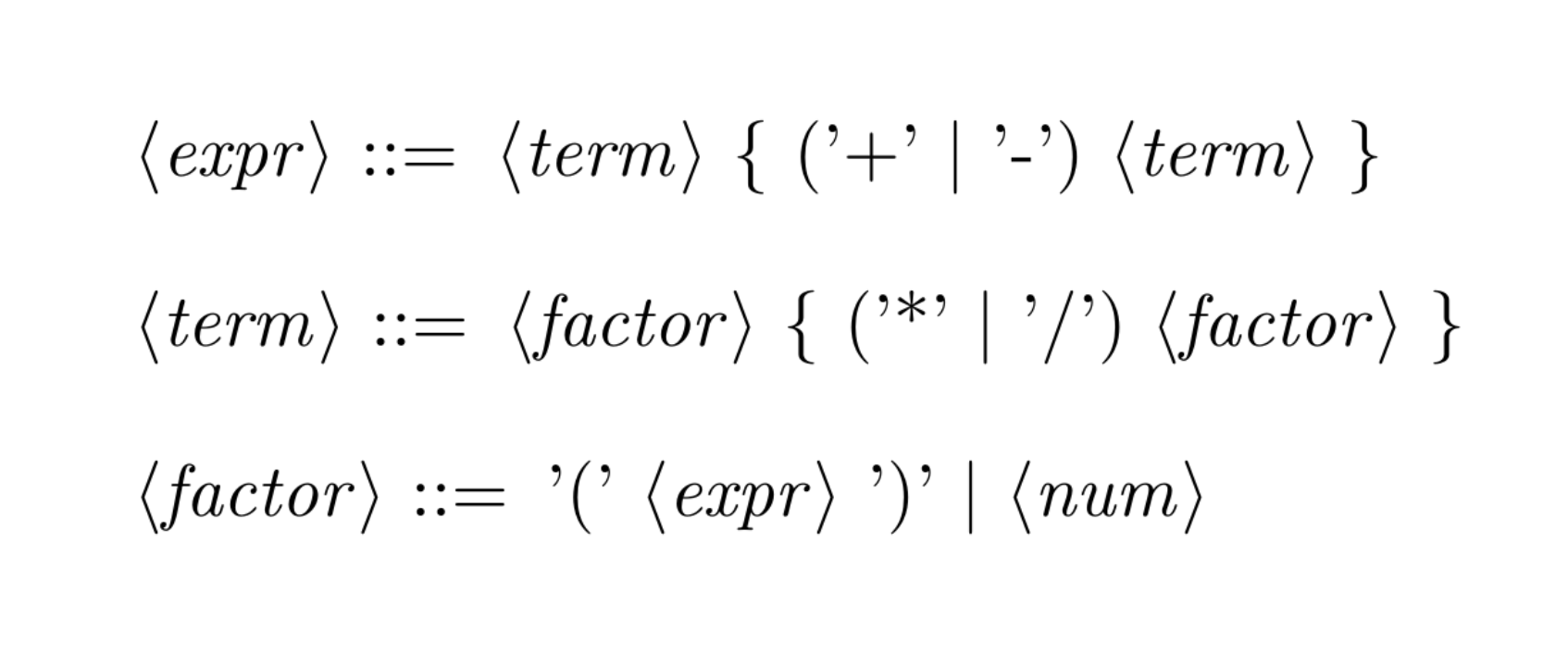
Instead of using algorithms like Shunting Yard or precedence climbing, the precedence of the operators is encoded directly in the various production rules. This is the simplest approach to take, but it works well in the implementation. Nora Sandler presents this method, and explains how to get there here on her blog. I recommend reading this article by Theodore Norvell if you want to learn more about paring expressions. It explains both the Shunting Yard algorithms and precedence climbing.

How would this grammar parse an expression like 7 + 42 * 9? It starts at 7, goes down the leftmost derivation of both expr and term, and then chooses the num alternative in factor. Next, + is consumed by the optionally repeated part of expr, and we go down another term, with 42 * 9 as the rest of the input. The recursion mechanism at work here defers the partial tree consisting of (+ 7 <term>) that we have parsed so far. Starting at 42, term now goes down the leftmost factor again. This factor becomes another num, consuming 42 from the input. Now * is consumed by the optionally repeated part of term, and then factor consumes the last numeric literal 9. In total, the second term in the expr production rule produces the tree (* 42 9). Now that the end of the input has been reached, this tree is used to complete the first partial tree. This way we get (+ 7 (* 42 9)) as the result.

Implementation

We’ll use the Megaparsec library of parser combinators for our implementation. The Megaparsec tutorial is quite thorough, and I recommend you give it a read if you want to use Megaparsec.

First off, let’s define a representation of the ASTs we wish to create:

-- Expr.hs

data Expr
  = Add Expr Expr  -- +
  | Sub Expr Expr  -- -
  | Mul Expr Expr  -- *
  | Div Expr Expr  -- /
  | Num Int
  deriving (Show, Eq)

The first Expr represents the left-hand side of the binary expressions, and the second Expr represents the right-hand side.

Next, we’ll need to define some helpers to start parsing. Here we mostly use the combinators found in Control.Applicative and in Megaparsec’s Lexer module.

-- Expr.hs

import Data.Void
import Control.Applicative hiding (many)
import Text.Megaparsec
import Text.Megaparsec.Char
import Text.Megaparsec.Char.Lexer as L

data Expr = -- [...]

type Parser = Parsec Void String

spaceConsumer :: Parser ()
spaceConsumer = L.space space1 empty empty

pSymbol :: String -> Parser String
pSymbol = L.symbol spaceConsumer

pLexeme :: Parser a -> Parser a
pLexeme = L.lexeme spaceConsumer

pNum :: Parser Expr
pNum = Num <$> pLexeme L.decimal

pSymbol and pLexeme consume all white space after they are parsing. They don’t consume initial white space, so be careful about that. Now we can already parse numbers.

λ :l Expr
[1 of 2] Compiling Main             ( Expr.hs, interpreted )
Ok, one module loaded.
λ parseTest (pNum <* eof) "7"
Num 7
λ parseTest (pNum <* eof) "43587"
Num 43587
λ parseTest (pNum <* eof) "blah"
1:1:
  |
1 | blah
  | ^
unexpected 'b'
expecting integer
λ parseTest (pNum <* eof) "92 * 4"
1:4:
  |
1 | 92 * 4
  |    ^
unexpected '*'
expecting end of input

As you can see, different numbers are all parsed correctly and invalid inputs are rejected with nice error messages generated by Megaparsec.

Let’s now start implementing the parser. We’ll build it up from the bottom, starting with factor.

-- Expr.hs
-- [...]

inParens :: Parser a -> Parser a
inParens = between (pSymbol "(") (pSymbol ")")

pFactor :: Parser Expr
pFactor = inParens pExpr <|> pNum

pExpr :: Parser Expr
pExpr = undefined

How do we define pExpr? It should parse a single term, and then go on to parse an infinite number of plus or minus characters, each followed by another term. term has the same shape as expr, so once we know how to implement expr, we can also implement term. Parsing the first term is simple:

-- Expr.hs
-- [...]

pTerm :: Parser Expr
pTerm =  -- [...]

pExpr :: Parser Expr
pExpr = do
  lhs <- pTerm
  -- ...

A parser that parses a + or a - and then parses another term might look like this: ((pSymbol "+" $> Add) <|> (pSymbol "-" $> Sub)) <*> pTerm. It discards the symbol it parsed and instead returns the value constructor of the expression that belongs to that symbol. Then it applies the expression parsed by the pTerm on the right to that value constructor. But there is an problem here though! The term that’s applied to the value constructor first is the right-hand side of the binary expression. But the first parameter of the value constructor is defined to be the left-hand side. We need to flip the parameters of the value constructor.

-- Expr.hs

import Data.Functor (($>))

-- [...]

pExpr :: Parser Expr
pExpr = do
  -- lhs :: Expr
  lhs <- pTerm
  -- rhs :: Expr -> Expr
  rhs <- flip <$> pOperator <*> pTerm
  pure $ rhs lhs
  where
	pOperator = (pSymbol "+" $> Add) <|> (pSymbol "-" $> Sub)

Let’s try it out again.

λ :l Expr
[1 of 2] Compiling Main             ( Expr.hs, interpreted )
Ok, one module loaded.
λ parseTest (pExpr <* eof) "92 * 4"
1:7:
  |
1 | 92 * 4
  |       ^
unexpected end of input
expecting '+', '-', or digit

It doesn’t work yet, because we’re missing the zero or more repetitions part. For this, many can be used, which will run the given parser zero or more times and return a list of all results. In our case, it returns a list of Expr -> Expr. A left fold can be used to apply the functions in this list to another, starting with lhs. This will build the desired left-associative tree of expressions.

-- Expr.hs
-- [...]

pTerm :: Parser Expr
pTerm = do
  lhs <- pFactor
  rhs <- many $ flip <$> pOperator <*> pFactor
  pure $ foldl (\expr f -> f expr) lhs rhs
  where
    pOperator = (pSymbol "*" $> Mul) <|> (pSymbol "/" $> Div)

pExpr :: Parser Expr
pExpr = do
  lhs <- pTerm
  rhs <- many $ flip <$> pOperator <*> pTerm
  pure $ foldl (\expr f -> f expr) lhs rhs
  where
    pOperator = (pSymbol "+" $> Add) <|> (pSymbol "-" $> Sub)

Now it works! I formatted the GHCI output a bit so it’s easy to recognize that the trees in the output match those from the beginning of this post.

λ :l Expr
[1 of 2] Compiling Main             ( Expr.hs, interpreted )
Ok, one module loaded.
λ parseTest (pExpr <* eof) "92 * 4"
Mul (Num 92) (Num 4)
λ parseTest (pExpr <* eof) "7 + 42 * 9"
Add
	(Num 7)
	(Mul
		(Num 42)
		(Num 9))
λ parseTest (pExpr <* eof) "2 * 3 / 4 * 5"
Mul
	(Div
		(Mul
			(Num 2)
			(Num 3))
		(Num 4))
	(Num 5)
λ parseTest (pExpr <* eof) "8 * (10 - 6)"
Mul
	(Num 8)
	(Sub
		(Num 10)
		(Num 6))

Conclusion

pTerm and pExpr are very similar and can easily be abstracted into a function that parses any left-associative binary expression. Then, the production rule for any level of precedence can be implemented in a single line. Unary operators can also be added by extending pFactor.

The code for this post can be found here. It includes such a generic function for parsing expressions.

I hope this post managed to convey my enthusiasm about the elegance of paring by recursive descent in Haskell! Feel free to reach out (email) if you find this interesting too, or if you have any questions/suggestions about the implementation presented here.